什么是倍频程?
- 音频杂谈
- 2023-05-28
- 65热度
- 0评论
噪声测量经常用到倍频程,有时在振动测量中也要用到倍频程,按照理论公式定义的倍频程中心频率不可能全是整数,但相应的标准中给出的中心频率全部都是整数,这是为什么呢?在这主要介绍以下内容:
1. 倍频程的定义;
2. 怎么计算中心频率;
3. 倍频程标准中心频率;
4. 倍频程的计算。
1. 倍频程的定义
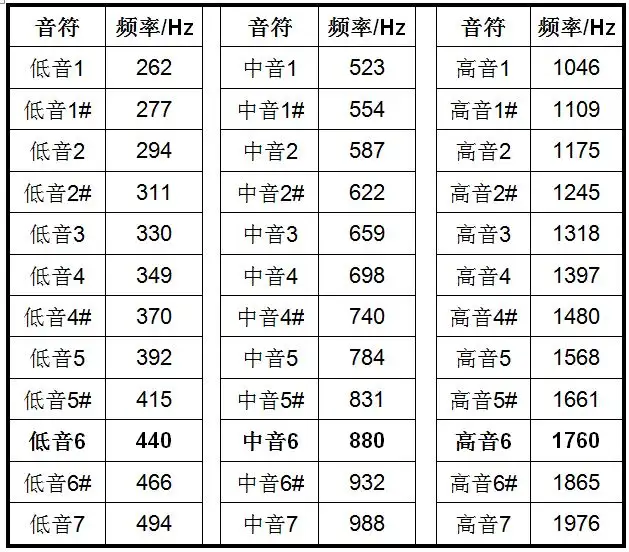
先让我们来看一下C调音符与频率对照表,如下表所示,考虑每一行,你会发现中音对应的频率是低音对应频率的2倍,高音对应的频率是中音对应的频率的2倍,而我们知道一个1/1倍频程(以下倍频程指1/1倍频程)宽度的上限频率是下限频率的2倍。因此,倍频程来源于音乐理论。
C调音符与频率对照表
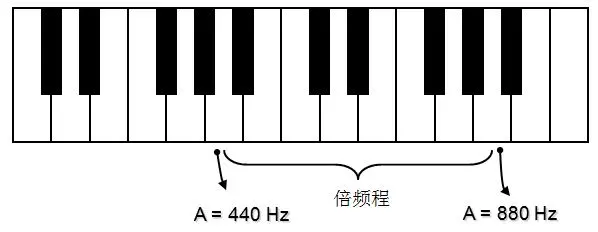
同一个音符的低音与中音,中音与高音之间相差八个音符,这一点从钢琴的琴键上更易于确认,如下图所示。下图中选取的频率区间是低音6#到中音6#所对应的琴键,中间刚好相差八个键,即八个音符,也就是说一个倍频程对应一个八音符跨度。
每个倍频程带都有一个中心频率与上限和下限频率,如下图所示,每个框代表一个倍频程带,框的左右边界代表上下限频率,中心竖线代表该倍频程带的中心频率。上限与下限频率也称为这个倍频程带的最大与最小频率,且二者之比为2:1。

各倍频程带中心频率fc与上、下限频率(fl和fu)的关系如下
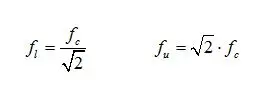
将以上关系再整理可得到
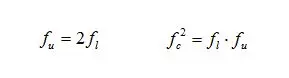
一个倍频程带可以再划分为三个等比宽度的频带,也就是我们常说的1/3倍频程,如下图所示。
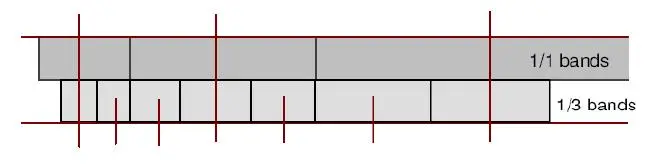
1/3倍频程带各中心频率fc与上、下限频率(fl和fu)的关系如下
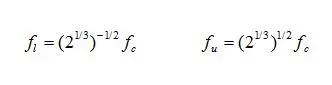
将以上关系再整理也可得到类似倍频程的关系
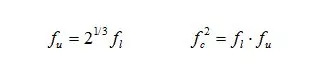
因此,对于1/N(N=1,2,3,6,12,24等)倍频程而言,每个频带的中心频率与上下限频率的关系为
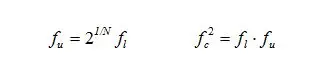
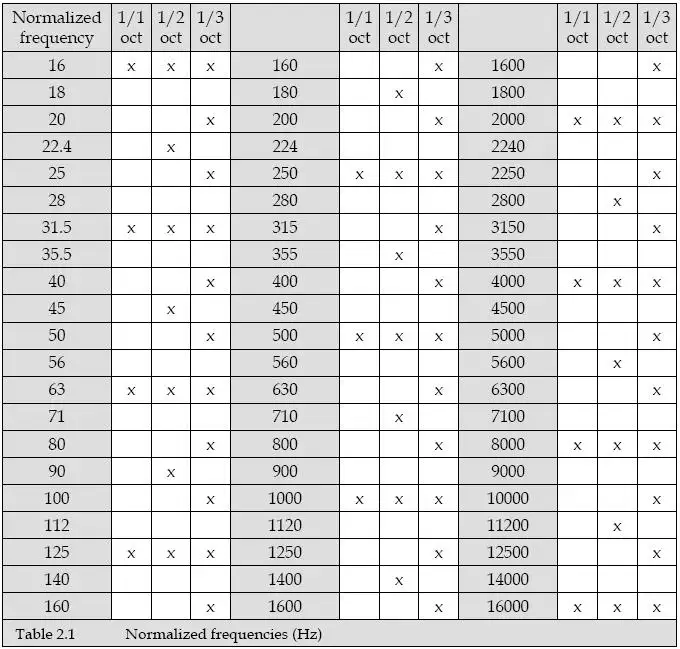
ISO标准150266或者国标GB 3420都已经将倍频程进行了标准化,下图为ISO标准150266按1、1/2和1/3倍频程对20KHz频带内划分的中心频率,×表示相应频带内的中心频率。但在我国基本上不用1/2倍频程。
2. 怎么计算中心频率
上一节的公式只是表明了中心频率与上下限频率之间的关系,并没有说明是如何确定各个频带的中心频率的。在声学中,频率1000Hz是非常重要的,例如它被确定为响度级——方的基准频率(见国标GB 3239《空气中声和噪声强弱的主观和客观表示法》)。因而,规定频率1000Hz为声学测量中所用频率系列的基准频率。ISO和ANSI已认可的两种方法中各频段的中心频率已明确定义。
一种方法是采用2为基数,相邻两个中心频率之比为
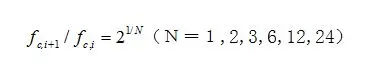
当N=3时为1/3倍频程,其他倍频程类似。此时相应的倍频程的各个中心频率计算公式如下
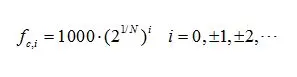
另一种方法是采用10为基数,相邻两个中心频率之比为
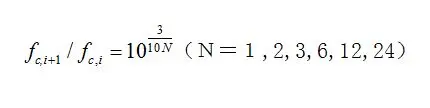
这个比率也可以写成
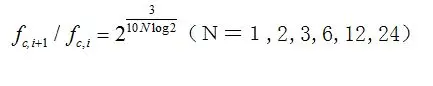
此时相应的倍频程的各个中心频率计算公式如下
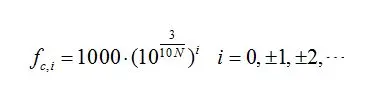
对同一个倍频程而言,两个方法的比率几乎相同,但是如果对频带边界上的单频信号感兴趣,不同的方法可能导致这些信号出现在不同的倍频程带中。基数2使用更简单,但是基数10实际上是更加合理的数值。在国标GB3240《声学测量中的常用的频率》中采用的就是基数10的方法。
按以上两种方法计算1-20KHz内的中心频率,如下表所示。从该表中可以看出,两种方法计算得到的各个中心频率很接近,但不相等(1000Hz除外);两种方法计算得到的绝大多数中心频率与标准值不相等。由于两种方法计算出来的中心频率不相等,因此,各个中心频率对应的倍频程带的上下限频率必然有差异。
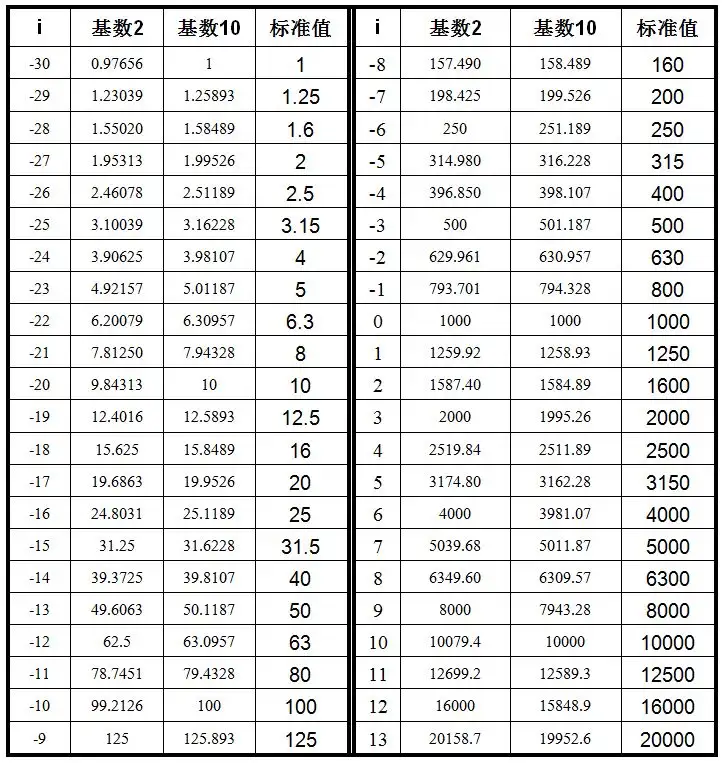
使用基数10,一个非常好的理由是10的幂的倍频程的中心频率(1,10,100,1000和10000)都是精确相同的,而基数2的中心频率却不是这样(但在125,250,500,1000,2000,4000,8000和16000处是精确相同的,似乎精确相同的数还多于方法基数10)。如果我们使用基数2的方法去计算1/3倍频程频带100Hz处的理论上的中心频率,得到的结果是99.21257…,但是如果用基数10计算得到的结果是精确的100Hz。如果我们继续向下到10Hz和1Hz,那么基数2对应的中心频率分别为9.84313…和0.97656…Hz。基数10得到的结果是精确的10Hz和1Hz。需要注意的是这些低频的中心频率两种方法之间的差异近似于1/24倍频程。
通常声学方面的工作不太关心这些非常低的频率成分。这就解释为什么这些标准要使用1000Hz作为基准中心频率,而不是逻辑上的1Hz。如果1Hz用作基准频率,那么在1000Hz处,两种方法将出现严重的差异,这在声学上是非常重要的。
举例说明计算方法不同带来的差异,对于基数为2的1/3倍频程1000Hz以下的一个理论上的中心频率是1000除以2^1/3,其值为793.7005。使用基数为10相应的中心频率为794.3282。两种方法下最近的标准值是800Hz,这个便是标准中所定义的中心频率。当计算1/3倍频程带边界频率时,分别使用以下公式计算
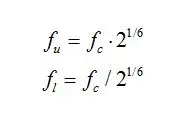
此时的中心频率是精确的理论值(如793.7005),而不是标准值(800)。对于1/N倍频程的边界频率计算公式如下
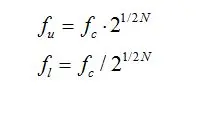
我们仍然计算这个中心频率的上下限频率。基数2的中心频率为793.7005,上下限频率为707.1068和890.8987;基数10的中心频率为794.3282,上下限频率为707.666和891.6033。因此,采用不同的方法计算得到的精确的中心频率和上下限频率是有差异的,如果刚好关心边界频率,则不同的方法会导致这个频率落在不同的倍频程带中。
由于标准中使用的是以10为基数的方法计算得到的,因此,软件中可能默认的方法也是以10为基数,但实际上,可以更改,像LMS Test.Lab修改界面如下图所示。
3. 倍频程标准中心频率
通过上一节的计算,我们已经明白两种方法计算得到的各个中心频率与标准中给出的标准值都不相同(1000除外),这是为什么呢?
倍频程的“标准”中心频率(即上表中的标准值)是基于优先数(Preferred numbers)。这些所谓的优先数起源于19世纪法国陆军工程师Col.Charles Renard(1849-1905)当时的工作是改进军方捕捉的气球数去观察能量位置。这项工作的结果产生了后来知名的雷纳德数(Renard numbers)。优先数在1965年被英国标准化,对应的标准为BS2045:1965优先数,1973年ISO(ISO 3-1973《优先数——优先数系列》)和ANSI也给出了相应的版本。优先数并不是特定用于1/3倍频程,他们广泛用于宽带应用中,包括电容和电阻、建筑工业和零售包装业等。
首先让我们明白一下什么是优先数,它们起什么作用。在工业设计行业,产品开发必须选择一些长度、距离、直径、体积和其他一些特征量,而所有这些选择的特征量都受功能、实用性、兼容性、安全或成本等因素的约束。这时选择的这些尺寸通常采用的数就是所谓的优先数。不同的人在不同时期设计产品时,优先数能增大产品之间的兼容性,有助于减少制造不同尺寸的产品。如某单位要生产4种不同尺寸的螺杆,长度位于10-100mm之间,那么选择16mm、25mm、40mm和63mm将在一定程度上能保证满足客户的需求,减少浪费,这些尺寸数值就是优先数。
在英标BS2045中,这些优先数被称作为R5,R10,R20,R40和R80等数列。用字母“R”是为了感谢1870年法国陆军工程师雷纳德所做的第一手工作。
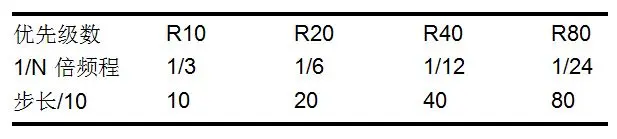
下面的R80数值列表给出了1/24倍频程10Hz以内的优先频率值。对于1/12倍频程每跳过1个数得到一个相应的优先值1.0,1.06,1.12等;对于1/6倍频程每跳过3个数得到一个相应的优先频率值1.0,1.12,1.25等;对于1/3倍频程每跳过7个数得到一个相应的值1.0,1.25,1.60等;对于1/1倍频程每跳过23个数得到一个相应的值1.0,2.0,4.0等。对于1/3倍频程,我们已知的标准值序列为:1.0,1.25,1.6,2.0,2.5,3.15,4.0,5.0,6.3,8.0,10…
1/24倍频程1到10Hz的优先数值(R80)
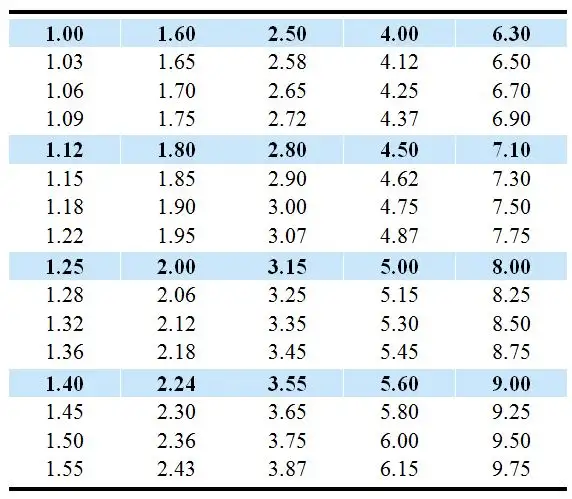
因此,标准中定义的各个倍频程的中心频率并非上一小节中两种方法计算得到的数值,而是按以上规则选择的相应优先数作为“标准”中心频率。
4. 倍频程的计算
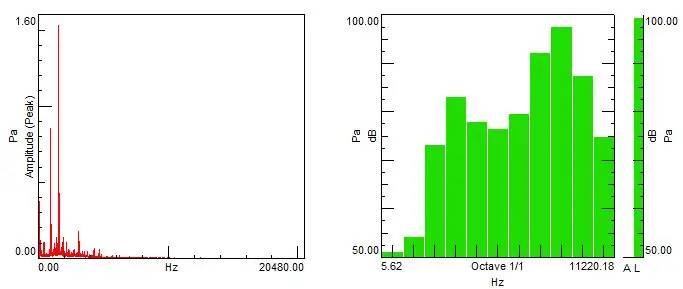
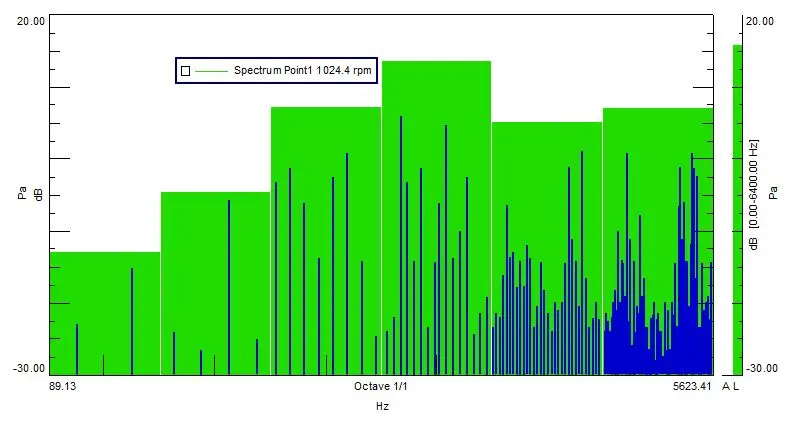
如下图所示为一个噪声信号的频谱图和1/1倍频程图,是怎样由频谱得到倍频程的呢?左图是由一条条谱线所组成,而右图是由相应的倍频程带组成。
在进行倍频程计算时,根据相应的方法(基数10还是基数2)来确定各个倍频程带的上下限频率(倍频程带),因此,相应倍频程带内的谱线数也就确定了。各个倍频程(1/N倍频程)带内的声压均方值是该频带内频谱谱线幅值的均方值之和:
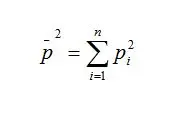
pi是各条谱线的均方根值,然后再对上式计算分贝值
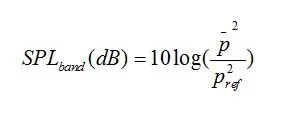
用倍频程(1/N倍频程)表示的总声压均方值则是各个倍频带内的均方值之和
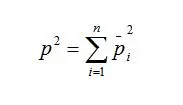
然后对此值按上面公式计算分贝值则是总声压级,即上面右图右侧的柱状线(L计权值)。倍频程(1/N倍频程)的谱密度,即均方值/Hz,则是这个倍频带的均方值除以相应的带宽。
因此,倍频程表示的是相应倍频程带内的声能之和,如下图所示。蓝色线条表示相应的频谱成分,由于高频段倍频程带越宽,因此,相应的谱线越密集。从这幅图也可以看出,当倍频程用于噪声测试时,是评价一个完整倍频程内的噪声平均幅值,常用于分析宽带噪声,突显不出主要的频率成分。
关于优先数和雷纳德数更多详情,请参阅:
